TEORIA E PRÁTICA NO ENSINO DA MATEMÁTICA: Ensino de Frações no 5º Ano do Ensino Fundamental
Eliany Lenz Wiirzler[1]
RESUMO
Não é raro, ainda em nossos dias, ouvirmos de estudantes as seguintes afirmações: eu não gosto de matemática, não sei para que aprender isso. Ou, para que aprender isso, esses montes de números e letras nunca me serão úteis. Uma matemática descontextualizada, principalmente nas primeiras séries, tem dificultado a absorção de seus conceitos. Muitos alunos não conseguem ver conexão entre o que é ensinado na escola, com o que ele vive em seu dia a dia. Conforme exposto no PCN’s (1998) os alunos chegam ao terceiro ciclo do Ensino Fundamental sem uma clara compreensão dos diferentes significados da representação fracionária e decimal nos números racionais. Esse trabalho teve por objetivo mostrar que é possível trabalhar a matemática, de maneira especial as frações, de forma que o aluno consiga visualizá-la na sua vida diária. É possível transformar conteúdos difíceis e abstratos em algo prazeroso e contextualizado. A metodologia utilizada foi a pesquisa qualitativa, com o uso de técnica de análise bibliográfica. Apoiado por autores consagrados como D’Ambrósio (1996), Tiba (2006), Moura (1996), entre outros, chegou-se à conclusão de que existe um campo muito pouco explorado pelos educadores, na contextualização, na ludicidade, no concreto, nos jogos matemáticos, que muito pode auxiliar no processo de ensino das frações.
Palavras chave: ensino, ludicidade, prática, frações.
- INTRODUÇÃO
Ensinar matemática exige mais que conhecimento, exige desejo e prazer de estudar e compartilhar aquilo que se aprendeu. Como também exige técnicas específicas de desenvolver no educando a mesma paixão presente no professor. Muito se pode saber sobre como resolver problemas, sobre a origem do conceito matemático, mas se essas teorias não forem transmitidas de forma dinâmica, não farão sentido na vida do educando e então a matemática perde o sentido de ser.
Os professores podem se esforçar ao máximo tentando incutir na mente de seus alunos, fórmulas, regras, teoremas e maneiras de chegar a uma solução para o problema, porém devem se esforçar ainda mais para promover sentido diante do que estão estudando, mostrando que a disciplina de matemática é útil e indispensável no dia a dia de cada um deles.
Para uma boa aula de matemática o professor deve conhecer suas raízes, saber de onde surgiram os cálculos para então ensinar de forma contextualizada, não somente lançando regras sem sentido, mas mostrando de onde vieram tais questões e o que se quer com elas, porém não se deve permanecer somente no passado, mas trazer a disciplina para a atualidade, de forma que os alunos de hoje compreendam a importância da matemática na história e que consigam utilizá-la de forma inteligente no presente. D’Ambrósio (1996, p. 30) afirma que: ... “conhecer as teorias e práticas que ontem foram criadas e que serviram para resolver problemas de ontem pouco ajuda nos problemas de hoje”. Sendo assim, como podemos perceber o conhecimento da história é importante sim para localizar o educando, mas a repetição de fórmulas sem sentido não ajudará no crescimento do educando atual, pois de nada adianta o educador ter todo conhecimento sobre a história da matemática, se não consegue relacioná-la com o presente e mostrar que essa deve fazer sentido na vida do educando.
D’Ambrósio (1996, p. 30) nos dá um vislumbre disso através de um pequeno poema narrativo de Dschuang Dsi, completado e divulgado por René Thom, que diz assim:
Havia um homem
Que aprendeu a matar dragões e deu tudo o que possuía
Para se aperfeiçoar na arte.
Depois de três anos
Ele se achava perfeitamente preparado mas,
Que frustração, não encontrou
Oportunidades de praticar sua habilidade.
(Dschuang Dsi)
Como resultado ele resolveu
Ensinar como matar dragões.
(René Thom)
O poema acima pode ser visto como a narrativa da vida de um estudante de matemática que mais tarde se torna professor. Ele inicia o curso de maneira empolgada, se envolve, se empenha para aprender ao máximo tudo o que está sendo ensinado e dá tudo o que possui para terminar o curso. Dá seu tempo, talento, finanças, empenho e ao final de três anos, o tempo de duração do curso universitário, acha que está perfeitamente preparado para fazer um bom trabalho em sala de aula, que está pronto para desenvolver as suas funções, que tem conhecimento suficiente, pois conhece a história da matemática, suas fórmulas e cálculos necessários.
Porém esse mesmo estudante de matemática se sente frustrado, chateado, pois não encontrou formas de ensinar aquilo que aprendeu, porque via a matemática como algo frio e pertencente a um passado longínquo, distante da atual realidade que circunda seus então alunos, pois estes não se interessam pelo que ele quer ensinar.
Diante disso, René Thom completa a narrativa, esse antes aluno e agora professor, passa a ensinar da mesma forma que aprendeu. Coloca a matemática na vida de seus pequenos educandos de forma fria, descontextualizada e sem sentido, de maneira que nenhuma das duas partes se sintam satisfeitas com o resultado, mas o faz para não perder o investimento feito durante alguns anos da sua vida. Por isso esse artigo se faz importante, para levar o leitor a compreender que a matemática pode ser viva, divertida e que pode ser utilizada no dia a dia, pois muito conhecimento, domínio de conteúdo sem uma utilidade prática, não vai fazer de quem ensina um bom professor.
D’Ambrósio (1996, p.29), ainda afirma que diante de um ensino baseado “... em coisas acabadas, mortas e absolutamente fora do contexto torna-se cada vez mais difícil motivar alunos para uma ciência tão cristalizada”.
Tudo o que se aprende no ensino superior, as teorias da matemática, as teorias de ensino só terão valor se, quando utilizadas na sala de aula produzam resultados satisfatórios. Todo conhecimento acumulado ao longo dos anos, se não puder ser levado para dentro do ambiente escolar, onde as transformações reais acontecem, onde a sociedade deposita sua confiança de uma melhoria significativa na vida de seus filhos, não terá nenhum sentido, e se desaparecer não fará falta.
D’Ambrósio (1996, p. 43) afirma:
O valor da teoria se revela no momento em que ela é transformada em prática. No caso da educação, as teorias se justificam na medida em que seu efeito se faça sentir na condução do dia-a-dia na sala de aula. De outra maneira, a teoria não passará de tal, pois não poderá ser legitimada na prática educativa.
Principalmente, para que o ensino da matemática se torne mais atrativo, e consiga motivar seu estudo, é necessário que o que se ensina tenha significado no dia a dia de quem aprende. Dirigir o ensino da matemática para situações, de convivência dos alunos, apresentando a eles como essa disciplina é utilizada em cada movimento seu, em cada projeto idealizado por eles, pode fazer uma grande diferença, pelo menos na motivação e expectativa em relação ao aprendizado.
- O ENSINO DA MATEMÁTICA HOJE
Diante do exposto podemos entender que a matemática deve ser contextualizada e levada para dentro da realidade da escola, pois é uma das disciplinas mais importante na vida de um educando, sendo fundamental para o desenvolvimento mental do indivíduo, pois através dela se desenvolve o raciocínio lógico da pessoa.
O conhecimento matemático deve e é utilizado em várias outras áreas do conhecimento e é essa desenvoltura que os cálculos e estudos da matemática permitem ao educando, pois exercita o cérebro. Segundo D’Ambrósio (1996, p. 44).
Parece de fundamental importância e o que representa o verdadeiro espírito da Matemática é a capacidade de modelar situação real, codificá-las adequadamente, de maneira a permitir a utilização das técnicas e resultados conhecidos em um outro contexto, novo.
A história da matemática é importante sim, mas a maneira como é ensinada, utilizada na atualidade é que faz a diferença, pois deve estar ligada ao cotidiano, fazendo sentido para quem estuda, dentro de uma nova realidade. (PAIS, 2006, p. 27) afirma:
a contextualização do saber é uma das mais importantes noções pedagógicas que deve ocupar um lugar de maior destaque na análise da didática contemporânea. Trata-se de um conceito didático fundamental para a expansão do significado da educação escolar. O valor educacional de uma disciplina expande na medida em que o aluno compreende os vínculos do conteúdo estudado com um contexto compreensível por ele.
O aluno precisa encontrar nessa disciplina razão para aprender e não ´aprender por aprender´. A matemática deve fazer parte da significação real do educando, esse deve saber em qual momento da sua vida está utilizando ou já utilizou os conceitos matemáticos, dessa forma a disciplina passará a ser prazerosa e importante, assim a aprendizagem acontecerá de maneira efetiva.
Quando o aluno perceber a sua necessidade pessoal da matemática, isso é, quando compreender que essa faz parte intrínseca da sua vida passará não só a vê-la como uma disciplina obrigatória e chata, mas como uma necessidade para os seus negócios, afazeres domésticos, lazer, enfim, perceberá que a matemática faz parte da sua vida em qualquer instancia. Segundo Tiba (1998, p.105) o professor ganhará muito quando conseguir mostrar que a matemática está unida à vida prática do educando, pois este muitas vezes tem conhecimento técnico, mas não tem sabedoria por não exercitar o cérebro.
Na atualidade o aluno tem acesso a muitos meios de conhecimento, apenas nem sempre consegue sistematizar o aprendizado. Estão conectados à multimídia, internet, televisão, e outros tipos de canais de informação, não sendo mais um “repetidor” do que ensina o professor. Por isso o professor deve instruir seus alunos na busca pelo conhecimento contextualizado, utilizando aquilo que ele já conhece com a teoria da matemática, colocando-a dentro da sua vida cotidiana.
A informação a um clique de distância exige que o professor prepare melhor suas aulas, trazendo para a sala novas maneiras de apresentar velhos conceitos.
Ainda, segundo Tiba (2006), não funciona mais a figura do professor detentor do poder, autoritário, que não admite que o mundo mudou.
As escolas e os professores que se acomodam, não se preocupam com as novas expectativas de seus alunos os estão perdendo ou os convidando a se retirar. Essas escolas estão perdendo a oportunidade de formar bons cidadão e os relegando à marginalização.
- HISTÓRIA DAS FRAÇÕES
Segundo Boyer (1996) a utilização dos números, através de contagem oral foi ficando cada vez mais ampla até que o ser humano sentiu a necessidade de exprimi-los de algum modo. Talvez começando como uma linguagem de sinais, começando pela utilização dos dedos das mãos e depois acrescentando os dedos dos pés, pequenas quantidades eram facilmente expressas. Quando os dedos não eram suficientes utilizavam montes de pedras para representar quantidades maiores. Essas pedras eram amontoadas em grupos de cinco, pois já estavam familiarizados com os múltiplos de cinco, pela observação da mão e dos pés. Num estudo de várias tribos de índios americanos, observou-se que quase um terço utilizava a base decimal, e aproximadamente outro um terço usava a base quinaria ou quinaria-decimal. E em cerca de dez por cento das tribos era utilizada a base vigesimal, e menos de um por cento usava em sistema ternário.
O surgimento do número inteiro, segundo Boyer (1996) se perde nos tempos da pré-história, porém a noção de fração surgiu muito tempo depois. Em vez de usar frações a humanidade utilizavas unidades muito pequenas, o que supria a sua necessidade.
Na obra de Boyer (1996) encontram-se trechos do Livro II das Histórias de Heródoto nas quais ele diz que o rei Sesótris, distribuiu a terra às margens do Nilo entre todos os egípcios com o objetivo de cobrar impostos. Para facilitar o processo foi dada a cada um deles uma porção igual de terra. Mas no período das chuvas, o rio inundava partes dessas terras, o que causava reclamações de seus proprietários na hora de recolher seus tributos. Foi então que o Rei ordenou que seus medidores encontrassem uma forma de descobrir o quanto cada propriedade perdia de suas terras, para poder calcular com justiça a taxa anual exigida. A unidade de medida padrão utilizada pelos seus medidores, que também eram chamados de “estiradores de corda”, para fazer as medições da terra era a unidade de Faraó, o cúbito ou côvado. O comprimento do cúbito era equivalente à distância compreendida entre a ponta do dedo médio e o cotovelo do faraó. As cordas dos estiradores possuíam diversos nós, cuja distância entre dois nós consecutivos era a medida do cúbito, o que hoje seria aproximadamente 45 cm.
Dias & Moretti (2011, p. 120) afirma que “a corda com vários nós compunha um instrumento de medida, uma ‘régua’ primitiva utilizada por agrimensores daquela época”. Para chegar à medida do terreno, os agrimensores da época esticavam a corda medindo o perímetro do terreno, e transformavam a medida em cúbitos para que as taxas fossem cobradas. Mas nem sempre as medidas coincidiam com o cúbito inteiro, então foram criadas divisões menores da medida, ou seja, os cúbitos foram fracionados. Essa foi, provavelmente a primeira forma de frações da humanidade.
Dessa época para cá o mundo mudou e a matemática acompanhou essa evolução. Novas técnicas foram se tornando necessárias. Novos cálculos se tornaram essenciais para acompanhar o avanço das tecnologias. As frações também foram sendo cada vez mais utilizadas e com maior complexidade, conforme a exigência das novas formas de ver o mundo, novas formas de comércio, medidas fracionadas. Por isso, a necessidade de uma boa base, já nos primeiros anos escolares, na compreensão e utilização das frações.
- A MATEMÁTICA NA ESCOLA
A matemática está inserida em quase tudo o que está ao nosso redor. Nos meios de transportes há matemática, na comida que comemos, no telefone celular, na televisão que assistimos, na casa que moramos, ou seja, em quase tudo há matemática. Apesar disso, em muitas aulas a matemática parece estar dissociada do dia a dia. Moyses, (1997, p.67) afirma que:
Se professor e alunos defrontam-se com sentenças, regras e símbolos matemáticos sem que nenhum deles consiga dar sentido ou significado a tal simbologia, então a escola continua a negar ao aluno – especialmente àquele que frequenta a escola pública – uma das formas essenciais de ler, interpretar e explicar o mundo. O importante é que o aluno, ao chegar a utilizar tais notações simbólicas, compreenda a sua razão de ser.
Sendo assim, ensinar matemática como um fim em si mesmo faz dessa disciplina algo inatingível para grande parte dos alunos que encontra muita dificuldade para guardar fórmulas e conceitos vazios, sem sentido. Situações problemas fazem o aluno pensar, pois as respostas não estão explícitas, necessitando que o aluno busque formas de chegar à resposta fazendo suas próprias operações. Como relata o PCN’s (1998, p. 32):
O ponto de partida da atividade matemática não é a definição, mas o problema. No processo de ensino e aprendizagem, conceitos, ideias e métodos matemáticos devem ser abordados mediante a exploração de problemas, ou seja, de situações em que os alunos precisem desenvolver algum tipo de estratégia para resolvê-las.
O aluno desenvolve seus saberes matemáticos por repetição e memorização, por meio de uma sequência de conteúdos encadeados do mais fácil ao mais difícil, do concreto ao abstrato, a partir da manipulação de objetos, exploração e vivências de situações que envolvem o raciocínio lógico matemático. Este usa aprendizados já adquiridos para absorver conteúdos mais complexos (cognição). Elas constroem seus conhecimentos matemáticos por meio de sucessivas reorganizações ao longo das suas vidas. Elaboram uma série de ideias e hipóteses provisórias antes de compreender um objeto em toda sua complexidade. Então pode surgir a dúvida: Como trabalhar a matemática no cotidiano escolar?
Segundo os estudiosos o professor deve proporcionar situações cotidianas, programadas ou espontâneas que encorajem os alunos a pensarem sobre os saberes matemáticos necessários, além de trocar ideias com os colegas para entender sua lógica. Isso pode acontecer em rodas de atividades, jogos, brincadeiras, rotina, culinária, cantos, resolução de conflitos etc.
- ENSINO DE FRAÇÕES: CAMINHO ABERTO À LUDICIDADE
Mesmo sendo um conteúdo fundamental para a compreensão da matemática, bem como sua utilização muito necessária nos cálculos, as frações nem sempre se tem dado o devido valor ao seu ensino. Aulas extremamente abstratas têm dificultado a compreensão, por parte do educando, de sua lógica. Até por isso no PCN’s (1998, pp. 100 e 101) propõe:
Embora a representação fracionária e decimal dos números racionais sejam conteúdos desenvolvidos nos ciclos iniciais, o que se constata é que os alunos chegam ao terceiro ciclo sem compreender os diferentes significados associados a esse tipo de números e tampouco os procedimentos e cálculo, em especial os que envolvem os racionais na forma decimal.
Assim, conclui-se que é necessária uma atenção especial ao ensino deste conteúdo, utilizando-se de cada recurso disponível, a fim de que se abra um caminho para a compreensão mais clara, e uma fixação, daquilo que é ensinado, no aprendizado dos alunos.
A utilização de material concreto no ensino de frações oferece a oportunidade aos alunos de ativar em sua mente a prática criadora. Deixar que os alunos resolvam questões com material palpável, pois incentiva o pensamento lógico, auxiliando-os no processo de autoaprendizagem. Grando (2004, p.21) afirma:
A matemática existe no pensamento humano e, por isso, depende de muita imaginação para definir suas regularidades e conceitos. Torna-se necessário aos processos pedagógicos considerar a importância de se ampliar a experiência das crianças a fim de proporcionar-lhes momentos de atividade criadora.
Aulas monótonas com o professor discursando o tempo todo, exigindo silêncio, como sendo uma autoridade absoluta, ou mesmo como professor liberal, que tudo permite, têm tirado dos alunos a oportunidade de desempenhar um papel criativo na construção dos saberes matemáticos. O relacionamento de confiança e respeito entre alunos e professores tem influência no grau criativo e de aprendizagem dos alunos. Segundo Brotto (1997, p. 67): “Quando conseguimos nos descontrair e ficar mais flexível nas nossas interações com os outros, liberamos todo o potencial criativo que há em cada um.”
Usar atividades lúdicas no ensino de frações, muitas vezes consegue quebrar o paradigma de que matemática é uma disciplina muito difícil, complicada, pois o educando consegue facilmente associar o conteúdo explicado com os conceitos matemáticos que está aprendendo. Conceitos distantes da realidade dos alunos dificultam a aprendizagem.
(Smole & Diniz & Cândido, 2000, pg. 16). afirma:
De fato, enquanto brinca a criança pode ser incentivada a realizar contagens, comparar quantidades, identificar algarismos, adicionar pontos que fez durante a brincadeira, perceber intervalos numéricos, isto é, iniciar a aprendizagem dos conteúdos relacionados ao desenvolvimento do pensar aritmético.
As frações dentro da matemática é um dos assuntos que mais dá oportunidade ao uso da ludicidade, porém não é um conteúdo entre os mais comuns dentro dos muros escolares. Os alunos nem sempre conseguem desenvolver as atividades de frações de maneira correta e seu pouco uso ou explicação a torna distante da realidade do aluno.
Porém mostraremos algumas atividades lúdicas que poderão, de alguma forma, auxiliar o professor no processo de formação de seus alunos, tornando a aula de matemática, dentro do assunto de frações, uma aula mais prazerosa e participativa.
Atividade 1
Dominó das frações
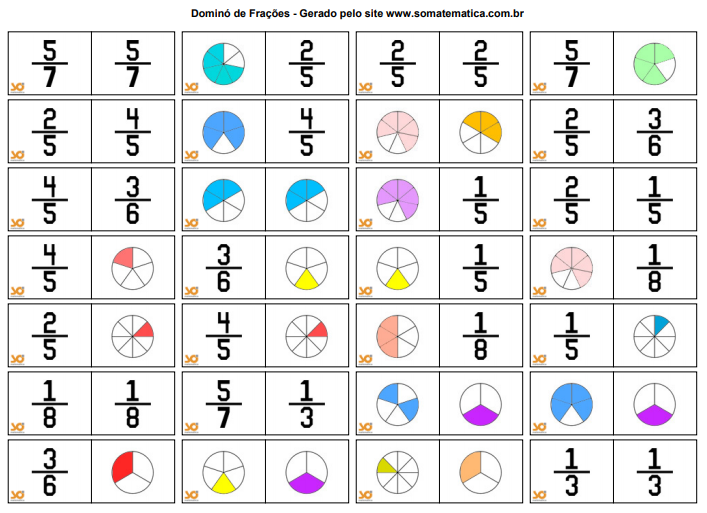
Atividade 2
- Pesquisar a que Estado cada time do campeonato brasileiro de futebol 2018 pertence;
• Separar os times por região;
• Separar os alunos por região;
• Representar a fração de times por região em relação ao todo.
Atividade 3
5º ano: chocolate e pizza – (Você vai precisar de um chocolate para cada aluno).
- Cada aluno deve abrir seu chocolate e contar quantos pequenos retângulos formam o todo.
- Peça para que cada um divida seu chocolate ao meio e, depois, quebre cada um dos pequenos retângulos que o formam.
- Trabalhe noções de equivalência (1/2 equivale a 6/12, por exemplo). Dificulte a atividade, pedindo a equivalência em pedaços do chocolate para 1/3, 1/4, 1/6.
4.Peça para os alunos dividirem seus chocolates em tamanhos diferentes (1/2, 1/3, 3/4 etc.) e depois peça para compararem os tamanhos com os dos colegas. Assim, eles vão perceber qual é maior. - Trabalhe também noções de soma de frações. Se somarmos 1/4 do chocolate com 1/2 do chocolate, quantos quadradinhos teremos? Qual será a representação dessa soma numericamente?
- Feito isso, peça para que os alunos entreguem 1 quadradinho para a professora e monte o chocolate inteiro. Elas vão perceber que, a cada quadradinho recebido, muda o numerador, mas o denominador continua igual.
- Assim que esse conceito estiver bem trabalhado, peça para que mais alguns (três ou quatro) alunos lhe entreguem um quadradinho. Assim, teremos uma situação em que o numerador passa a ser maior que o denominador. Ficará fácil para os alunos perceberem que isso é possível, já que é possível ter mais de um chocolate ao mesmo tempo.
Sugestão: Essa situação pode ser representada também com o modelo da pizza. Para isso, os alunos podem confeccionar uma pizza na aula de arte e, durante as aulas de matemática, usam tesoura e régua para dividir a pizza em fatias.
Uma variação dessa atividade também poderia ser juntar dinheiro com os alunos e fazer pizzas de verdade, e enquanto dividem as pizzas em frações, todos as saboreiam.
Atividade 4
Bingo das frações
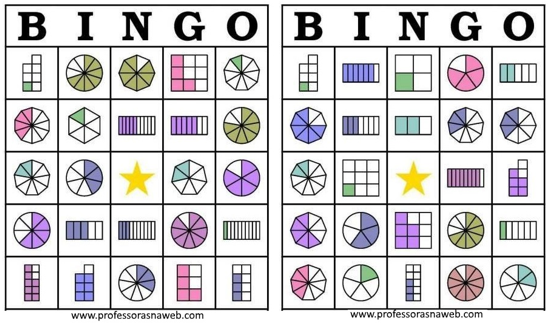
http://atividadespara4ano.blogspot.com/2016/11/jogo-bingo-das-fracoes-para-imprimir.html
A utilização de frações no dia a dia dos alunos, às vezes não passa de meia dúzia de ovos, meio kg de arroz, meia xícara de chá, frações muito simples. Mas, como vimos nas atividades acima, não precisamos utilizar, nas atividades concretas, apenas aquilo que o aluno está familiarizado no seu dia a dia, mas a partir do simples ir acrescentando novos conceitos, como frações própria e impróprias, frações equivalentes, etc.
O conteúdo dos números fracionários foi estabelecido a partir do objetivo que vise possibilitar ao cidadão um saber que lhe permita lidar também com os números não naturais que possam representar quantidades não inteiras, já que estas, com o desenvolvimento das relações sociais, passaram a fazer parte do cotidiano desse cidadão. Foi, portanto, a vida quotidiana que definiu este objetivo como significativo. Daí a definição de um conjunto de estratégias para possibilitar o acesso ao novo conhecimento não precisou muito. E desta maneira o ensino das frações ordinárias passou a fazer parte dos programas escolares. (MOURA, 1996, p. 30)
Segundo Moura et al, 2010, p. 90 “A atividade de ensino do professor deve gerar e promover a atividade do estudante. Ela deve criar nele um motivo especial para a sua atividade: estudar e aprender teoricamente sobre a realidade”.
Dessa forma, pensamos que através de atividades lúdicas como as propostas acima o aluno pode encontrar sentido na matemática e aprende-la de forma mais fácil, sentindo até mesmo prazer nesse ato.
CONCLUSAO
O estudo da matemática e das frações, nesse caso em especial é essencial no processo de ensino e aprendizagem e isso ocorre porque a matemática está diretamente ligada ao cotidiano das pessoas e as frações da mesma forma, pois ao se fazer uma receita de bolo, dividir alguma guloseima, encontramos medidas fracionárias.
Às vezes é estranho pensar em como uma disciplina tão presente no quotidiano dos alunos pode causar tamanha dificuldade de aprendizagem. Esse fato foi uma das causas consideradas para a elaboração de tal artigo, então buscamos explorar esse assunto de forma simples mostrando como uma boa didática pode facilitar a vida dos estudantes, levando os alunos a maior nível de compreensão do assunto “frações”.
Diante do exposto percebemos a grande responsabilidade que o professor tem diante da sociedade e com ele a própria instituição escolar, pois são estes dois agentes quem podem abrir ou fechar as portas do conhecimento para pessoas que estão iniciando a vida estudantil, pois “alunos e professores devem ter argumentos para respaldar os caminhos da matemática, esse exercício é fundamental para formar cidadãos que saibam questionar fatos, determinações, deveres e que saibam argumentar sobre seus direitos”. (MONTEIRO, 2011)
Reconhecemos que este trabalho ainda não está completo, pois existem muitas outras atividades que poderiam ser feitas para o ensino lúdico e contextualizado das frações, entretanto procuramos abordar esse assunto como uma prova de que existem maneiras de se trabalhar a matemática facilitando a sua compreensão e aprendizagem, oportunizando assim momentos únicos em que os alunos podem participar e refletir sobre o que estão aprendendo e dessa forma irem construindo o seu próprio conhecimento.
REFERENCIAS BIBLIOGRÁFICAS
BOYER, C. B. História da Matemática. 2ª ed. São Paulo: EdgardBlücher, 1996.
BRASIL/MEC, Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais. Brasília, 1998.
BROTTO, F. O. Jogos Cooperativos: Se o Importante é Competir, O Fundamental é Cooperar!. 3 ed. Santos: Projeto Cooperação, 1997.
D’ AMBROSIO, Ubiratan. Educação matemática: Da teoria à prática. Campinas, SP: Papirus, 1996.
DIAS, M. S.; MORETTI, V. D. Números e Operações: Elementos Lógicos-Históricos para a Aprendizagem. Curitiba: Ibpex, 2011.
GRANDO, R. C. O. Jogo e a Matemática no Contexto da Sala de Aula. São Paulo: Paulus, 2004.
GROENWALD, Cláudia L. Oliveira e FILIPPSEN, Rosane Maria Jardim. O meio ambiente e a sala de aula. Educação Matemática em Revista. (SBME), n.13, p36-40, 2003.
MOURA, M. O. et al. A Atividade Orientadora de Ensino Como Unidade Entre Ensino e Aprendizagem. In: MOURA, M. O. de (Coord.). A Atividade Pedagógica na Teoria Históricocultural. Brasília, DF: Líber Livro, 2010. p. 81 – 110.
MOURA, M. O. de. A Atividade de Ensino como Unidade Formadora. Rio Claro: Bolema, 1996.
MOYSES, Lucia, Aplicações de Vygotski a Educação Matematica. Campinas: Papirus, 1997.
MONTEIRO, Priscila http://matheusmathica.blogspot.com.br/2011/05/matematica-na-educacao-infantil.html acessado em 25/07/2018
PAIS, Luis Carlos. Didática da Matemática: Uma análise da influência Francesa. 2ª edição Belo horizonte: Autêntica, 2002
RIGON, A. J.; ASBAHR, F. da S. F.; MORETTI, V. D. Sobre o processo de humanização. In: MOURA, M. O. de. A atividade pedagógica na teoria histórico-cultural. São Paulo: Liber Livro, 2010.
SMOLE, K. S. DINIZ M. I. CÂNDIDO, P. Brincadeiras Matemáticas na Educação Infantil, vol 1. Porto Alegre: Artmed, 2000.
TIBA, Içami, Ensinar Aprendendo, Novos Paradigmas da Educação. São Paulo: Integrare, 2006.
TIBA, Içami. Ensinar aprendendo: como superar os desafios do relacionamento professor-aluno em tempos de globalização. São Paulo: Editora Gente, 1998.
http://3.bp.blogspot.com/-6f6lzNeYG2g/UCWVBvnA8eI/AAAAAAAATBk/-La8zFvi4tM/s1600/corrida+das+fra%C3%A7%C3%B5es+jogo+matem%C3%A1tica.jpg acessado em 15/07/2018
http://atividadespara4ano.blogspot.com/2016/11/jogo-bingo-das-fracoes-para-imprimir.html acessado em 15/09/2018
http://educacao.faber-castell.com.br/professores/na-sala-de-aula/contextualizando-saberes-matematicos-no-cotidiano-dos-alunos/ acessado em 04/04/2018
https://www.somatematica.com.br/softOnline/GeradorDominos/gerador.php acessado em 15/09/2018.
[1] Licenciada em Letras e Pedagogia. Pós-Graduada em Educação infantil com Ênfase em Educação Especial e Psicopedagogia Clínica e Institucional.



